How can machine learning solve my problem?

As machine learning researchers, there’s a question that we get asked in some form almost every day:

“How can machine learning solve my problem?”

In this book we answer this question by example. We do not just list machine learning techniques and concepts – instead we describe a series of case studies, all the way through from problem statement to working solution. Machine learning concepts are explained as they arise in the context of solving each problem. The case studies we present are all real examples from within Microsoft, along with an initial case study which introduces some core concepts. We also look at real problems encountered during each case study, how they were detected, how they were diagnosed and how they were overcome. The aim is to explain not just what machine learning methods are, but also how to create, debug and evolve them to solve your problem.

How does a model-based approach help?

When trying to solve a problem using machine learning, the fundamental challenge is to connect the abstract mathematics of machine learning to the concrete, real world problem domain. In this book we apply an approach called model-based machine learning. which focuses on understanding this connection. This understanding then helps with developing effective machine learning systems, interpreting their behaviour and solving the various problems that arise during the process.

The core idea at the heart of model-based machine learning is that all the assumptions about the problem domain are made explicit in the form of a model. In fact, a model is just made up of this set of assumptions, expressed in a precise mathematical form. These assumptions effectively build up a description of the world which can then be used to learn or reason about it. For example, in the next chapter we build a model to help us solve a simple murder mystery. The assumptions of the model include the list of suspects, the possible murder weapons, and the tendency for particular weapons to be preferred by different suspects.

In model-base machine learning, the model is then used to create a bespoke algorithm to answer a particular question about the problem domain, such as making a prediction or performing some reasoning. Model-based machine learning can be applied to pretty much any problem, and its general-purpose approach means you don’t need to learn a huge number of machine learning algorithms and techniques.

So why do the assumptions of the model play such a key role? Well it turns out that machine learning cannot generate solutions purely from data alone. There are always assumptions built into any machine learning algorithm, although sometimes these assumptions are far from explicit. Different algorithms correspond to different sets of assumptions. In cases when the assumptions are unclear, the only way to decide which algorithm will give the best results is to try each in turn. This is time-consuming and inefficient, and it requires software implementations of all of the algorithms being compared. And if none of the algorithms tried gives good results, it is even harder to work out how to create a better algorithm.

Models versus algorithms

Let’s look more closely at the relationship between models and algorithms. We can think of a machine learning algorithm as a monolithic box which takes in data and produces results. The algorithm must necessarily make assumptions, since it is these assumptions that distinguish a particular algorithm from any other. However, given just the algorithm, those assumptions are implicit and opaque.

Now consider the model-based approach. The model comprises the set of assumptions we are making about the problem domain. To get from the model to a set of predictions we need to take the data and compute those variables whose values we wish to know. This computational process is called inference. There are several techniques available for doing inference, as we shall discuss during the course of this book. The combination of the model and the inference procedure together define a machine learning algorithm, as illustrated in Figure 0.1.

Figure 0.1In the model-based view of machine learning, a custom algorithm is created by combining a model and an inference method. Here the coloured shapes within the model represent the assumptions comprising that specific model. Changes to the assumptions give rise to different machine learning algorithms, even when the inference method is kept fixed.

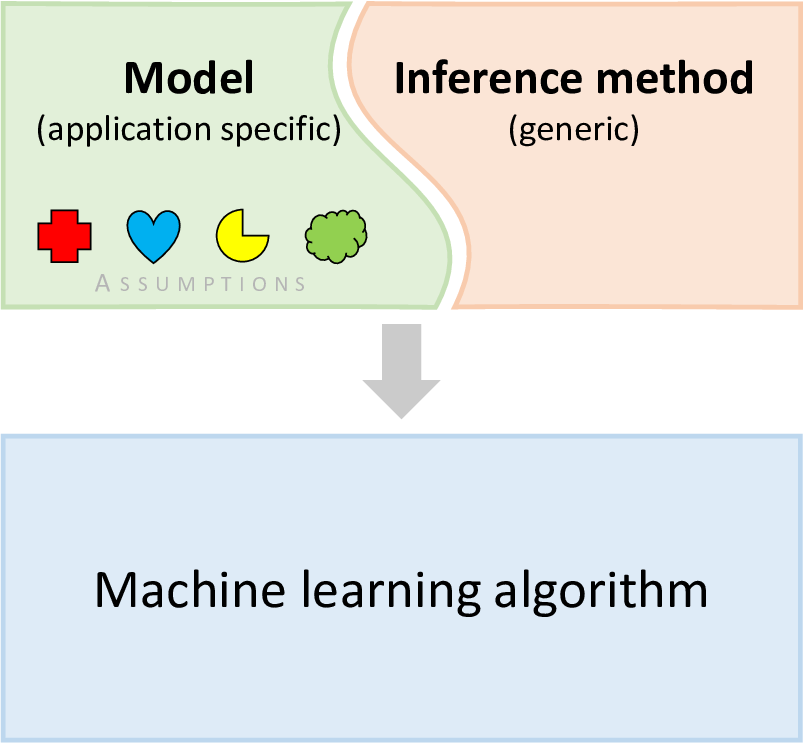
Although there are various choices for the inference method, by decoupling the model from the inference we are able to apply the same inference method to a wide variety of models. To illustrate this point, every single case study in this book will be solved using just one inference method.

Model-based machine learning can be used to do any perform machine learning task, such as classification (Chapter 4) or clustering (Chapter 6), whilst providing additional insight and control over how these tasks are performed. Solving these tasks using model-based machine learning provides a way to handle extensions to the task or to improve accuracy, by making changes to the model – we will look at an example of this in Chapter 4. Additionally, the assumptions you are making about the problem domain are laid out clearly in the model, so it is easier to work out why one model works better than another, to communicate to someone else what a model is doing, and to understand what’s happening when things go wrong. Using models also makes it easier to share other people’s solutions in order to adapt, extend, or combine them.

An example: deep learning

In recent years, deep learning has become the dominant approach to machine learning to such an extent that, to many people, deep learning is machine learning. What is less well known is that deep learning is an example of model-based machine learning, where the model being used is a neural network. Assumptions about the problem domain are encoded in the architecture of the neural network and in the choice of activation function for the neurons. No matter what neural network model is chosen, the same inference methods can be applied. For example, a neural network is usually trained using some kinds of stochastic gradient descent (SGD) method. Combining a particular neural network with SGD effectively gives a custom algorithm for training to solve a particular machine learning problem.

(a)

 

(b)

 

(c)

Figure 0.2In deep learning, different neural network models encode different assumptions about the task they are used for, illustrated here as different icons within each model. For example, the architecture of a neural network for object recognition encodes the assumption that objects look similar no matter where in the image they appear. Although the neural network models are different for different tasks, the same inference methods can be applied. Here, stochastic gradient descent (SGD) can be applied to train any of these models. Since the models are similar and the inference methods are the same, deep learning can be rapidly applied to new problem domains.

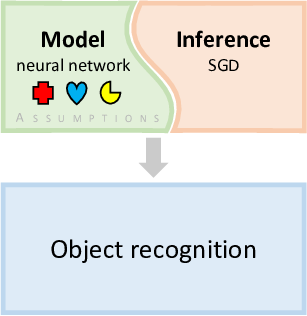
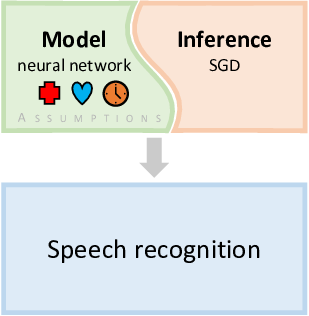
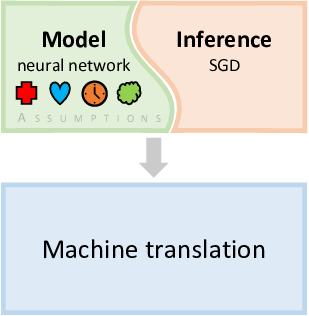
Figure 0.2 illustrates how deep learning has made use of model-based machine learning. One of the first breakthroughs in deep learning was when deep neural networks were used for object recognition in images [Krizhevsky et al., 2012]. The particular architecture of neural network chosen for this task encoded assumptions about the nature of objects in images – for example, that objects look similar no matter where in the image they appear. Combined with a suitable inference method, this gave a custom algorithm for object recognition which achieved unprecedented accuracy. For speech recognition this assumption does not make sense and so different architectures were used which made more appropriate assumptions – for example, that a particular word may be spoken quickly or slowly. However, other assumptions encoded in the form of the neural network were retained, since they are broadly applicable to many problem domains. The ability to retain many aspects of the neural network while making targeted changes has allowed deep learning to be applied to many different application areas relatively quickly , including machine translation [Sutskever et al., 2014]. Arguably, it is this ability, building on its model-based foundations, that has enabled the deep learning revolution.

Tools for model-based machine learning

The decomposition of an algorithm into a model and a separate inference method has another powerful consequence. It becomes possible to create a software framework which will generate the machine learning algorithm automatically, given only the definition of the model and a choice of inference method. This allows the applications developer to focus on the creation of the model, which is domain-specific, and frees them from needing to be an expert on the inner workings of the inference procedure.

For more than fifteen years we have been working on such a software framework at Microsoft Research, called Infer.NET [Minka et al., 2014]. Because a model consists simply of a set of assumptions it can be expressed in very compact code, which is relatively easy to understand and modify. The corresponding code for the algorithm, which is generally much more complex, is then produced automatically. All of the models in this book were created using Infer.NET, and the corresponding model source code is available online. However, these solutions could equally be implemented by hand or by using an alternative model-based framework – they are not specific to Infer.NET. Examples of alternative software frameworks that implement the model-based machine learning philosophy include BUGS [Lunn et al., 2000] and Stan [Stan Development Team, 2014].

As well as these general-purpose software frameworks, there has been enormous effort put in developing software specifically for neural network models, such as Tensorflow [Abadi et al., 2016] and PyTorch [Paszke et al., 2019]. Such frameworks embody the model-based machine learning approach by allowing the neural network to be described through a model description, such as in an ONNX file [Bai et al., 2019]. In this way, a custom neural network model can be trained or applied automatically, by any of the range of tools that support the ONNX format. This portability and ease-of-use are consequences of the model-based approach to machine learning.

Now that we have explained the concept of model-based machine learning, let’s see an example of it being used. On to the first case study!

[Krizhevsky et al., 2012] Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). ImageNet Classification with Deep Convolutional Neural Networks. In Neural Information Processing Systems, volume 25, pages 1097––1105.